When people talk about PBKDFs (Password Based Key Derivation Functions), this is usually either in the context of secure password storage, or in the context of how to derive cryptographic keys from potentially low-entropy passwords. The Password Hashing Competition (PHC, 2013-2015) was an open competition to derive new password hashing algorithms, resulting in Argon2 hash as its winner. Apart from achieving general hash security, many of the candidates focused on achieving resistance to parallel attacks on available hardware such as GPUs.
There exists, however, a somewhat less known password hashing primitive: a PBKDF with a special property, called delegation 1. In this blog post, we bring this primitive to attention and discuss its applicability in the context of End-to-End Encrypted (E2EE) backup systems. The idea is to be able to offload hashing computation to a potentially untrusted server.
In general, the higher the PBKDF’s work factor is, the more difficult it is to crack a password. Sometimes, however, the work factor is necessarily small; this happens if the system needs to support all devices, including the weakest of customer devices. Offloading to an untrusted server may allow increasing the work factor, preventing the factor being dictated by the weakest of customers’ devices.
Before moving on, let’s first disambiguate: in this blog post, we are not talking about PBKDF2, we are talking about any general Key Derivation Function that could typically be used for two different purposes. One purpose is to convert passwords to encryption keys and the other is to convert passwords into password hashes (used for authentication). PBKDF2 is just one example of such a function. Password hashing with delegation could aid both of those use cases, but in this blog post we focus on the encryption key derivation use case.
The basic scenario in which PBKDF with delegation may be considered is a login server that receives an authentication password and then delegates the password hash computation to another, untrusted entity.
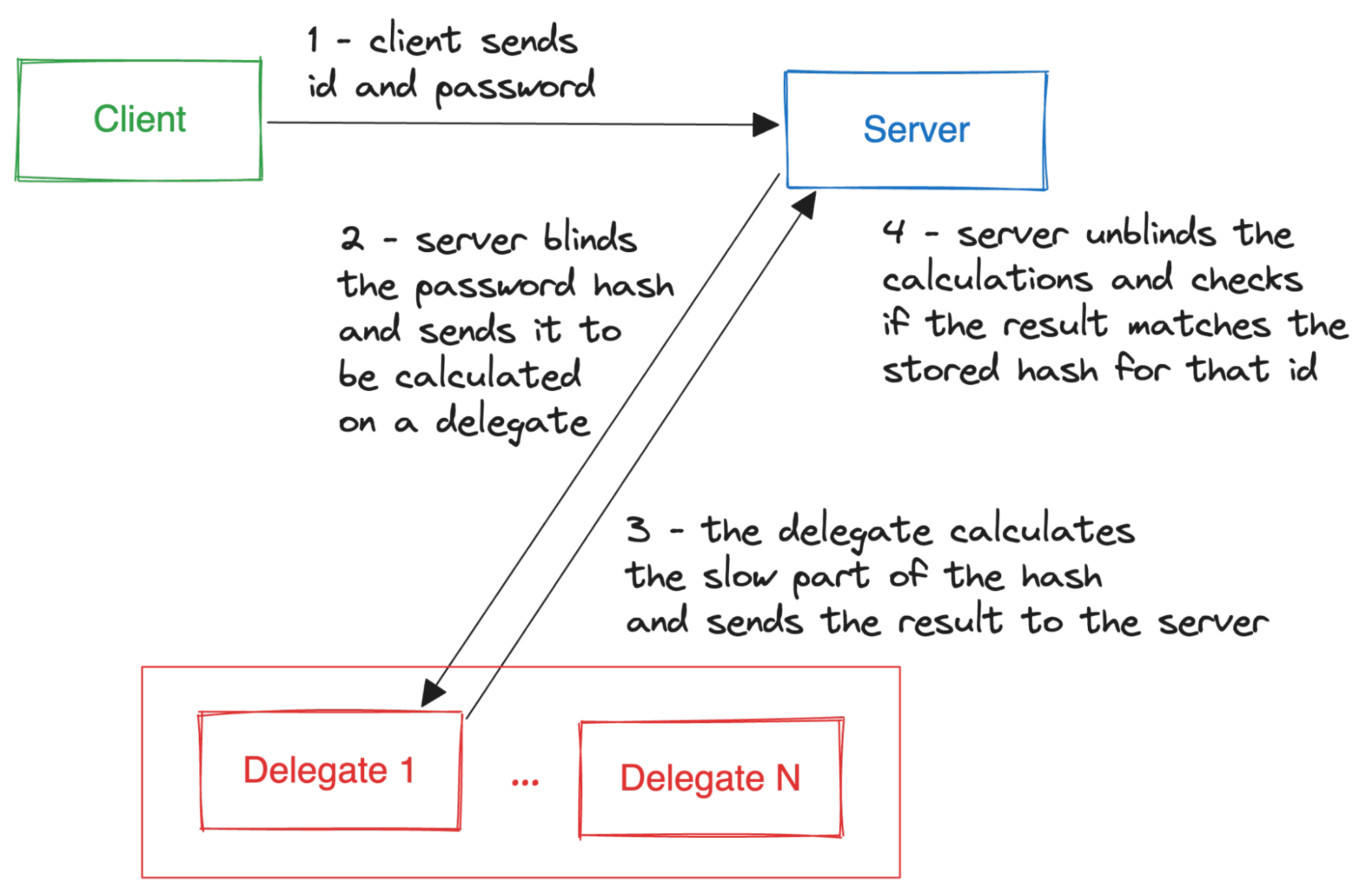
There is however a scenario that appears to further justify PBKDF delegation usage.
Recall the Firefox and Chrome “sync” features. These features offer users the option to save passwords, bookmarks and other browsing information on their provider’s servers. The Firefox sync is E2E encrypted by default, while Chrome saves the password and other data in plaintext on Google’s servers; only if the user modifies a browser setting, encryption is applied. In that case, servers do not get to see the plaintext data.
When it comes to the security of browser sync features, see this blog post together with further past discussions on the topic. Without going into details on what happens server-side, the client work factors in play when the user’s password is used to derive an encryption key are:
These parameters are lower than the currently recommended ones: 600000 rounds for PBKDF2 and N=32768 or N=1048576 for scrypt, depending whether it is interactive logins or file encryption. The reason for this is that the hash function work factors are dictated by the least capable subset of end-user devices; the feature should work on all devices and should not cause any disruption for a large device subset.
Let’s take a step back and list some of the E2EE backup systems out there. Such systems will have the client choose or generate a secret, from which a symmetric encryption key is derived. Data is encrypted client-side and sent to the potentially untrusted servers. There’s also the need to authenticate the user for encrypted data retrieval; the same or different secret may be used for that purpose.
Let’s try to categorize E2EE backup in terms of the amount of entropy users’ secrets have:
Password hashing with delegation would appear to make the most sense in the second case, that is, in systems that allow users to choose passwords and use those passwords to derive E2EE symmetric keys. In such cases, the (untrusted) server could be delegated to perform the hashing and the hashing work factor would no longer be dictated by the weakest of the client devices.
As for the first and the third case, if the passphrase already has high entropy, slow hashing is basically unnecessary. If the passphrase has low entropy (e.g. is a PIN), trust is already offloaded to the TEEs in the backend.
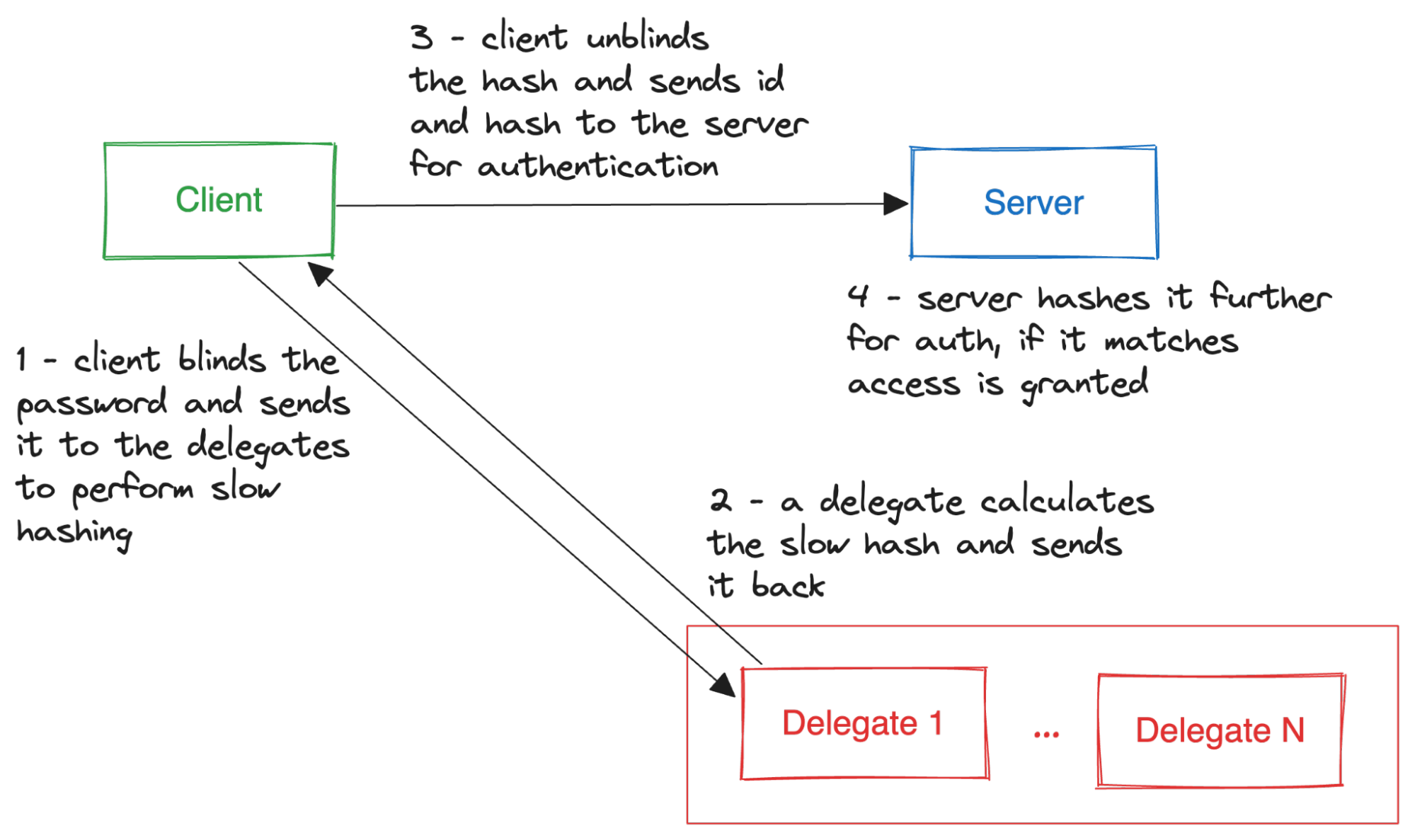
It is worth noting that the delegates in the picture could be owned by the backup provider itself.
The only hash function that supports delegation known to the author of this blog post is the Makwa hash function1. It was designed by Thomas Pornin and was a candidate to the Password Hashing Competition (PHC) which ran from 2012 to 2015. During the competition, it was found that a similar construction was independently discussed2 by Adam Back on the Bitcoin talk forum. Note that in the original Bitcoin talk post actually proposes the function for client-side hashing, in the context of so-called Bitcoin “brain-wallets”.
Here, we only discuss Makwa on a very basic level; there are some formulas below, but they are for illustration purposes only.
The idea is to convert the password into a value less than the RSA modulus $N = p\times q$, blind it with a secret factor and then apply a long sequence of Rabin encryptions. Alternatively, one could describe Makwa as a blind RSA computation with a very large exponent in the form of $e = 2^k$, for some work factor $k$.
Taking this into account, let’s do an exercise and try to derive parts of Makwa on our own. System A attempts to offload the computation to system B. System A derives $\pi$ from the password by using a KDF and salt; we don’t go into details of that here. The system A chooses a random blinding factor $\alpha\hspace{1mm}mod\hspace{1mm}N$ and sends $\alpha \times \pi\hspace{1mm}mod\hspace{1mm}N$ to system B. Suppose B takes on the work load and returns:
$$(\alpha \times \pi)^{2^k}\hspace{2mm}mod\hspace{2mm}N$$
The problem is that system A now needs to unblind $\alpha^{2^k} \times {\pi}^{2^k}\hspace{1mm}mod\hspace{1mm}N$. System A could perform the unblinding by computing $\alpha^{2^k}\hspace{1mm}mod\hspace{1mm} N$ and its inverse. However, this would be costly and it would defeat the original hash offloading purpose.
One could try to pre-compute the inverse of $\alpha^{2^k}\hspace{1mm}mod\hspace{1mm}N$ and keep the blinding factor constant, for all offloaded password hashings. This would not work, as it would leak information about passwords to the untrusted server.
To get around this, Makwa employs a technique based on the following idea. Generate a bunch of blinding factors $\alpha_i$ for $i = 1\ldots 300$, and pre-compute $(\alpha_i^{2^k})^{-1}\hspace{1mm}mod\hspace{1mm}N$ for all of them. Blinding is performed by multiplying $\pi$ with a randomly chosen subset of $\alpha_i$ values:
$$(\prod_{b_i = 1} \alpha_i) \times \pi\hspace{1mm}mod\hspace{1mm}N$$
where, for each $i$, $b_i$ is a random bit 0 or 1. System A can now efficiently un-blind, by multiplying the result with the corresponding pre-computed $\alpha_i$ values and choosing the $\alpha_i$ subset randomly makes it so that the blinding factors are unlikely to be repeated.
There’s an additional wrinkle to what we’ve been talking about. Squaring is not injective inside the multiplicative group modulo $N$, as both $x$ and $N - x$ get mapped to the same value. Squaring is injective, however, on the set of squares modulo $N$, if $N$ is a Blum integer, see the Properties section of this page.
If server B receives the password blinded as described by the previous equation, this value may or may not be a square. Server B could compute the Jacobi symbol of the received blinded value, despite the fact that the factorization of $N$ is not known. This would leak one bit of information on the indexes used for blinding. This does not appear to be a serious leak, but for safety and consistency, Makwa specifies that the server A squares both $\pi$ and the blinding factors before computing the value on which B will operate.
See Makwa’s specification for all the details on the function.
Sometimes, cryptography lets us achieve “magical” features that initially appeared impossible. This is indeed the case with hashing with delegation and Makwa. However, as a bonus, we may end up with additional properties that we don’t necessarily want, at least not in certain use-cases.
If factors $p$ and $q$ of $N$ are known, it is possible to rewind the slow hash computation back and derive the password derivative $p$. Depending on the Makwa hashing mode, this would mean either deriving a KDF of the password or the password itself. Also, if the factors are known, the hashing procedure can be sped up, making the hashing cost similar to the cost of one RSA private key operation.
In order to remove this possibility, $p$ and $q$ need to be securely discarded. This could be an obstacle for the E2EE backup setting. Users may question whether they are being backdoored by the E2EE backup provider. There does, however, exist a long thread of research on multi-party computation protocols for secure distributed generation of modulus $N$; a ceremony of that sort could be applied to derive the parameters.
Regarding concerns around lack of memory-hardness in the Makwa hash function, see this paper, which shows that the advantage GPUs have over CPUs is actually relatively small.
See also previous work on password peppering with delegation3 which is remotely related to hashing with delegation, but the employed techniques are different from those in Makwa.
Let’s end this blog post with a question:
We’d like to thank Iago Passos da Silva, Thomas Pornin, Filippo Valsorda, and Chris Bellavia for reviewing and discussing this blog post.
The Makwa Password Hashing Function, Thomas Pornin, https://www.bolet.org/makwa/makwa-spec-20150422.pdf ↩︎ ↩︎
Hardening brain-wallets with a useful blind proof of work, Adam Back https://bitcointalk.org/index.php?topic=311000.0 ↩︎
The Pythia PRF Service, Adam Everspaugh, Rahul Chatterjee, Samuel Scott, Ari Juels, and Thomas Ristenpart, https://eprint.iacr.org/2015/644 ↩︎